And there are 2 such triangles per side or 2n for the whole polygon. All sides are equal.
4 x 12 cm.
Formula of a regular polygon. Properties of a regular polygon. An angle outside the polygon formed by one of its sides and the extension of an adjacent side is. To find the area of a regular polygon you use an apothem a segment that joins the polygons center to the midpoint of any side and that is perpendicular to that side segment HM in the following figure is.
Area of Regular Polygon Formula A polygon having equal sides ie. Calculate the area of a regular pentagon with side 12 cm and apothem of 75 cm. If you know the length of one of the sides the area is given by the formula.
The formulas below give the length of the side of regular polygon given the number of sides and either the radius or apothem. N 2 180. Geometry Select an Item 2D Geometry 3D Geometry Area Chord Length Circle Circumscribed Solids Diagonal Formula Inscribed solids Perimeter Regular Polygon Surface Area Volume Perimeter of Regular Polygon can be calculated by adding the length of all sides.
The apothem of a regular polygon is a line segment from the centre of the polygon to the midpoint of one of its sides. Given the length of a side. The circle that goes all the way round the outside.
Most require a certain knowledge of trigonometry not covered in this volume but see Trigonometry Overview. A regular polygon is equilateral it has equal sides and equiangular it has equal angles. Properties of Regular Polygon - result 1.
Area of regular polygon where p is the perimeter and a is the apothem. For example if the interior angle was 165 subtracting it from 180 would yield 15. Find the perimeter of a regular polygon having four sides each measuring 12 cm.
If the regular polygon has an EVEN number of sidesthen the longest diagonal is the same as the diameter of the circumscribed circle - ie. Apothem is a segment that joins the polygons center to the midpoint of any side and it is perpendicular to that side. As we know Perimeter P n x s here n 4 s 12 cm.
The image above is of a regular hexagon inscribed in circle C with radius rAssume that the length of s is 4 units long. Determine the area of the regular hexagon above. The formula for calculating the size of an interior angle is.
6 x 45 m. Triangle 3 2 180. Regular Polygon - definition Regular polygon has its all sides equal.
The Longest Diagonal Formula. Finding the area of regular polygon when the SIDE and APOTHEM are known. An apothem is also used sometimes to find the area of a regular polygon.
A regular polygon is a polygon where all the sides are the same length and all the angles are equal. Area of Polygon ½ n Radius 2 sin2 πn Area of Polygon ¼ n Side 2 tanπn A Table of Values. The perimeter is just the length of one side multiplied the by the number of sides n.
Equiangular is known as a regular polygon. Perimeter of Regular Polygon P. An angle inside the polygon at one of its vertices is called the interior angle.
Subtract the interior angle from 180. Equilateral and equal angles ie. Some of the regular polygon formulas related to polygons are.
Angle Q is an interior. The number of sides of a regular polygon can be calculated by using the interior and exterior angles which are respectively the inside and outside angles created by the connecting sides of the polygon. Developing Formulas Learning Outcome.
Side length given the apothem inradius If you know the apothem distance from the center of the polygon to the midpoint of any side - see figure above where. Again the formula for a regular polygon is 12 times the apothem multiplied by the perimeter. Interior angle of a polygon sum of interior angles number of sides.
By definition all sides of a regular polygon are equal in length. All angles are equal. In Euclidean geometry a regular polygon is a polygon that is equiangular all angles are equal in measure and equilateral all sides have the same length.
In the MM book The Perfect Sausage and other Fundamental Formulas there are two formulas for longest diagonal of a regular polygon. Regular polygons may be either convex or starIn the limit a sequence of regular polygons with an increasing number of sides approximates a circle if the perimeter or area is fixed or a regular apeirogon effectively a straight line. For a regular polygon n also represents the number of triangles that make up the figure.
Find the perimeter of a regular polygon having six sides each side measuring 45 m. Area of Polygon n Apothem 2 tanπn When we dont know the Apothem we can use the same formula but re-worked for Radius or for Side. A is the length of the apothem inradius n is the number of sides.
The sum of the measures of the interior angles of a convex polygon with n sides is. In this lesson we will develop general formulas for finding areas of regular polygons. As the polygon is a pentagon having five sides where each side s measures 12 cm its perimeter p is 5 x s 5 x 12 60 cm Now as we know.
Exterior Angle Sum Property of Polygon - formula Exterior angle of polygon n 3 6 0 o Where n Number of sides of polygon. As we know Perimeter P n x s here n 6 s 45 cm. All the interior angles in a regular polygon are equal.
Even though we know that all the exterior angles add up to. How to use the formula to find the area of any regular polygon.

Derivation Of Formula For Area Of Regular Polygons With Side And Apothem Youtube
So whats the area of the hexagon shown above.
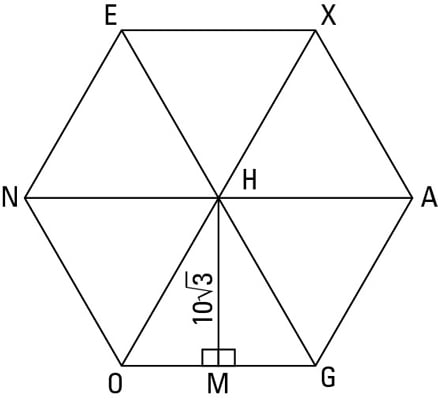
Formula for the area of a regular polygon. The area of the polygon is Area a x p 2 or 866 multiplied by 60 divided by 2. A regular pentagon has 5 equal sides. The apothem is calculated by its own formula by plugging in 6 and 10 for n and s.
Given the length of a side. Area ½ apothem perimeter Several other area formulas are also available. A regular polygon.
A regular polygon is a polygon where all the sides are the same length and all the angles are equal. By definition all sides of a regular polygon are equal in length. All the interior angles in a regular polygon are equal.
Length of apothem for a regular polygon having n sides s 2tanπ n s 2 tan π n. Where P is the perimeter of the polygon and r is the inradius equivalently the apothem. When we dont know the Apothem we can use the same formula but re-worked for Radius or for Side.
A regular polygon is special type of polygon. The area of any regular polygon is. The area of a regular polygon is given by the formula below.
Area of Regular Polygon. Find the area of a regular polygon with perimeter of 44 cm and apothem length of 10 cm. Therefore the area of the equilateral triangle is vor approximately 435 units The calculated areas are tan 30 n 87 rebo Then she used the formula for area of.
The perimeter is 6 x 10 n x s equal to 60 so p 60. Have pre-defined formulas for calculating their areas. The area of any regular polygon is equal to half of the product of the perimeter and the apothem.
Area of regular polygon where p is the perimeter and a is the apothem. Regular polygons such as rectangles squares trapeziums parallelograms etc. 220 cm 2.
The formula for calculating the sum of interior angles is n - 2 times 180circ where n is the number of sides. Equivalently it is both cyclic and equilateral or both equilateral and equiangular. The formula for calculating the size of an interior angle is The sum of the internal angles in a the regular pentagon fills approximately 07568 of its circumscribed circle.
Register free for online tutoring sessions. The apothem is 24142 centimeters. What is the Formula to Calculate the Area of a Regular Polygon.
Finding the area of regular polygon when the SIDE and APOTHEM are known. If you know the length of one of the sides the area is given by the formula. Area of Polygon ½ n Radius 2 sin2 πn Area of Polygon ¼ n Side 2 tanπn A Table of Values.
Here is a list of the sections within this webpage. The solution is an area of. Substituting the regular pentagons values for P and r gives the formula with side length.
The result of 2tan 1806 is 11547. To find the area of a regular polygon you use an apothem a segment that joins the polygons center to the midpoint of any side and that is perpendicular to that side segment HM in the following figure is an apothem. As shown below a regular polygon can be broken down into a set of congruent isosceles triangles.
If the length of one side is given it possible to find the area of the regular polygon by finding apothem. Most require a certain knowledge of trigonometry not covered in this volume but see Trigonometry Overview. In this case the hexagon has six of them.
Regular polygons may be either convex or starIn the limit a sequence of regular polygons with an increasing number of sides approximates a circle if the perimeter or area is fixed or a regular apeirogon effectively a straight line. ½ x 44 x 10 cm 2. Thank you for the challenge JubayerNirjhor.
Area of regular polygon where p is the perimeter and a is the apothem. In my next note I will prove that the area of any regular polygon can be represented as. And here is a table of Side Apothem and Area compared to a Radius of 1 using the formulas we have worked out.
Area of a regular polygon - derivation This page describes how to derive the formula for the area of a regular polygon by breaking it down into a set of n isosceles triangles where n is the number of sides. In Euclidean geometry a regular polygon is a polygon that is equiangular all angles are equal in measure and equilateral all sides have the same length. As we know Area A ½ x p x a here p 44 cm and a 10 cm.
The formula for the area of a regular polygon is given as A fracl2n4tanfracpi n Where l is the side length n is the number of sides. You use the following formula to find the area of a regular polygon. Formula for area of a regular polygon and compare it to Biancas answer.
The perimeter of the equilateral triangle is units. The apothem of a regular polygon is a line segment from the centre of the polygon to the midpoint of one of its sides. However for an irregular polygon the area is calculated by subdividing an irregular polygon into small sections of regular polygons.
The apothem rounded to the nearest tenth is units. Area of Regular Polygon.