2 2 4 2 2 4 2 8 256. 1 2 When n is a positive integer exponentiation corresponds to repeated multiplication of the base.
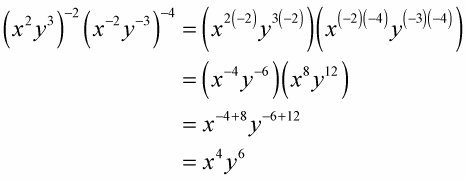
How To Raise Powers Of Powers Dummies
To get from 2-3 to 123 all you have to do is flip 21 it becomes 12 and change the sign of the exponent -3 to 3 and both still equal each other and equal the same answer 18.
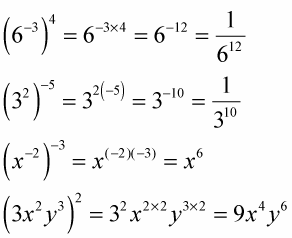
Exponent raised to an exponent. This is true for all kinds of exponents positive and negative and as we will see later fractional. Raising One Power to Another When one power is raised to another we multiply exponents. In 8 2 the 2 says to use 8 twice in a multiplication so 8 2 8 8 64.
A b n a n b n. 2 2 4 4 4 256. The last bit of code has the print function display both the original list values and those numbers raised to the 3rd power exponents.
2 4 2 8 2 64. An exponent also called a power is a compressed way of expressing repeated multiplications of a number by itself. An exponent of 75 means first raising to the seventh power and then finding the fifth root or first finding the fifth root and then raising to the seventh power.
3 4 3 3 3 3 81. This is what that displays. This exponent rule is often referred to as the power to power property.
Whenever you have an exponent expression that is raised to a power you can simplify by multiplying the outer power on the inner power. The base a raised to the power of n is equal to the multiplication of a n times. 1728 704969 -1953125 0086938307 2248091000 30080231000 1953125 157464.
A m n a m n EX. So since 2-3 is 18 and 123 is also 18 then. Exponents also known as powers are values that show how many times to multiply a base number by itself.
So the negative exponent just indicates that the base number 2 is now the reciprocal 12 - or flipped. In symbols given base b exponent e and modulus m the modular exponentiation c is. When multiplied bases are raised to an exponent the exponent is distributed to both bases.
The exponent of a number shows you how many times the number is to be used in a multiplication. C and exponents properties Like many things in mathematics there is a list of rules on how things behave when certain conditions are met. 8 2 8 8 64 In words.
A is the base and n is the exponent. The exponent of a number says how many times to use the number in a multiplication. 12 89 -125 0443 1310 3110 125 54 Raised to the power 3.
Any number raised to the power of 1 keeps the same value. Any number with an exponent of 0 is equal to 1. We seek to identify untapped potential navigate complexity and nurture positive relationships in order to unlock meaningful growth for our portfolio companies and investors.
A n a a. 3 3 3 3 3 27. Xm n x m n If you have a product inside parentheses and a power on the parentheses then the power goes on each element inside.
7 5 4 7 4 5 4 2401 625 38416 Exponent of 0. 3 1 3. Thus in this case you would raise 15 to the seventh power and then find that numbers fifth root.
When exponents are raised to another exponent the exponents are multiplied. Exponents rules and properties. To divide a fraction that is raised to an exponent give the exponent to both the numerator and the denominator.
Welcome to Exponent Exponent is a private equity firm that believes that greater understanding leads to greater transformation. That is b n is the product of multiplying n bases. 3 2 3 3 9.
For example 4 3 is telling you to multiply four by itself three times. From the definition of c it follows that 0 c m. 3 5 3 3 3 3 3 243.
What is an exponent. This also true for exponents for example zero-exponent property which states that anything raised to the 0 power is equals to 1. 8 2 could be called 8 to the power 2 or 8 to the second power or simply 8 squared Exponents are also called Powers or Indices.
C be mod m. On this lesson you will learn how to raise an exponent to another exponent. Exponentiation is a mathematical operation written as b n involving two numbers the base b and the exponent or power n and pronounced as b raised to the power of n.
First convert 14 to 1410 and reduce to 75. A n times. An exponent is a small number located in the upper right-hand position of an exponential expression base exponent which indicates the power to which the base of the expression is raised.
B-nm 1 bnm 1 mb n. X y z x z y z Example. 8 2 could be called 8 to the second power 8 to the power 2 or simply 8 squared.
4 3 4 4 4 64 The number being raised by a power is known as the base while the superscript number above it is the exponent or power. 45 4 4 4 4 4 1024. The operation of modular exponentiation calculates the remainder when an integer b the base raised to the e th power the exponent be is divided by a positive integer m the modulus.
The exponent of a number says how many times to use the number in a multiplication. Negative fractional exponents The base b raised to the power of minus nm is equal to 1 divided by the base b raised to the power of nm. What is an exponent.
If you like this Site about Solving Math Problems please let Google know by clicking the 1 button. By using this website you agree to our Cookie Policy.
Exponent Rules Dividing Exponents
Dividing zero exponents integer exponents negative exponents fractional exponents decimal exponents.
Exponent rules for division. What is an exponent. Power of a Power Rule. 1 Solving-Math-Problems Page Site.
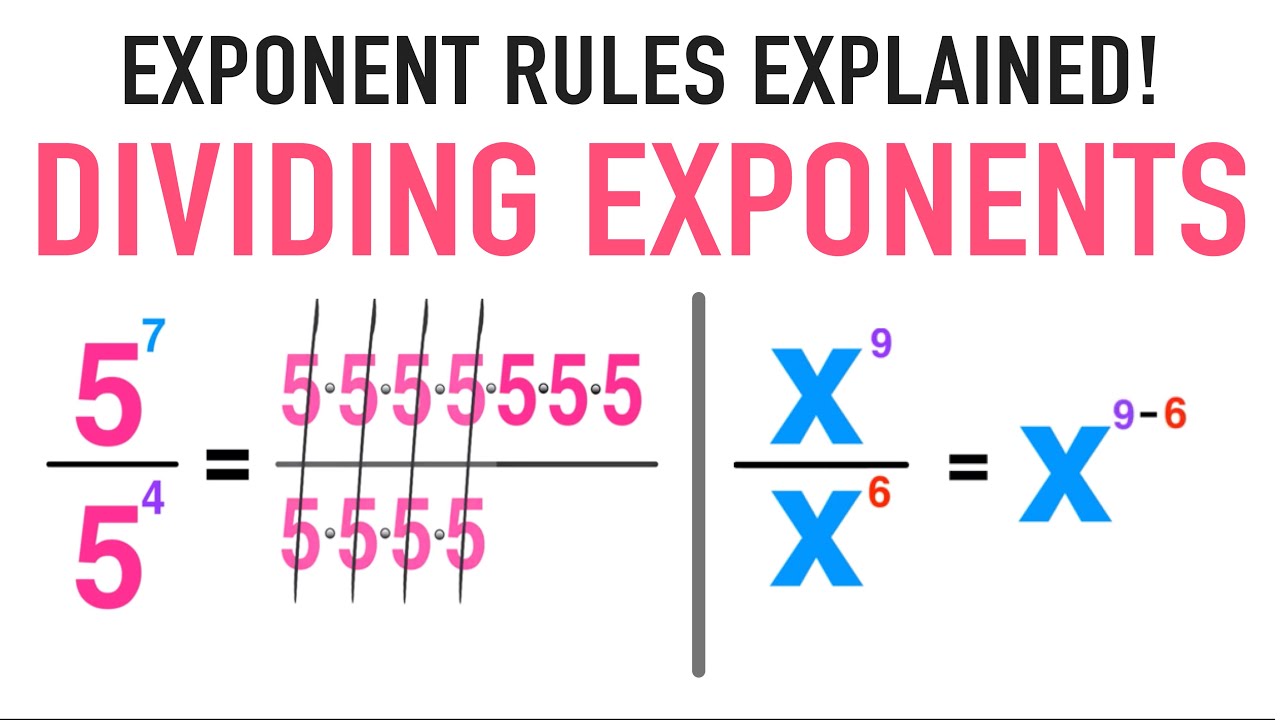
In other words theres another rule that also applies. Yes the rule you described does apply. To divide exponents or powers with the same base subtract the exponents.
As with many rules related to exponents writing out the exponents as multiplications makes it obvious why the rule is true 3332 333 33 35 33 32 3 333 3 35 12. When a power has an exponent keep the base the same and multiply the exponents. If the denominators exponent is negative you treat it as if it were positive and add it to the numerators exponent.
There are several other rules that go along with the power rule such as the product-to-powers rule and the quotient-to-powers rule. If a 1 button is dark blue you have already 1d it. Adding exponents and subtracting exponents really doesnt involve a rule.
Dividing exponents with different bases When the bases are different and the exponents of a and b are the same we can divide a and b first. 3 3 3 3. If a number is raised to a power add it to another number raised to a power with either a different base or different exponent by calculating the result of the exponent term and then directly adding this to the other.
Rules for multiplying and dividing. To divide exponents that have the same base keep the same base and subtract the power of the denominator from the power of the numerator. Power of a Power Property of Exponent.
The exponent rule for dividing exponential terms together is called the Quotient Rule. A is the base and n is the exponent. A n times.
If exponents have different bases you cannot subtract their powers. 62 4 62 3 62 4. Exponent rules laws of exponent and examples.
Dividing fractions with exponents with same fraction base. When youre subtracting exponents the same conclusion applies. Apply the division rule first and see if negative exponents show up again.
To divide exponents the exponents must have the same base andor the same power. If you like this Page please click that 1 button too. Simply calculate the result if.
The laws of exponents are defined for different types of operations performed on exponents such as addition multiplication and division. Division is the opposite of multiplication so it makes sense that because you add exponents when multiplying numbers with the same base you subtract the exponents when dividing numbers with the same base. The Quotient Rule for Exponents states that when dividing exponential terms together with the same base you keep the base the same and then subtract the exponents.
Abx ax bx. Dividing Fractional Exponents With the Same Base Tackle divisions of two numbers with fractional exponents by subtracting the exponent youre dividing the divisor by the one youre dividing the dividend. 2-3 5-2 5 2 2 3 25 8 3125.
A-n b-m b m a n. Free Exponents Division calculator - Apply exponent rules to divide exponents step-by-step This website uses cookies to ensure you get the best experience. 3 1 3.
When a number is multiplied by itself the exponents are formed. We will now consider combined operations of multiplication and division on numbers in exponent form using all the rules of exponents introduced above. The base a raised to the power of n is equal to the multiplication of a n times.
Review of simplifying expressions with exponents. When the bases and the exponents are different we have to calculate each exponent and then divide. The product of two powers with the same base is equal to that base raised to the sum of the two exponents.
A n b n a b n. What is an exponent. 3 2 3 3 9.
A m n a mn this says that to raise a power to a power you need to multiply the exponents. If thats the case utilize the negative rule of exponent. First of all the two positive numbers the bases have to be the same.
When an exponential expression is raised to a power copy the base which is a nonzero real number then multiply the inner and outer. If the exponential terms have multiple bases then you treat each base like a common term. A x a a 2 a x a x a a 3.
One way to simplify this is to ignore the negative exponents for now. A b n a b m a b n-m. However the answer is not just ab9 because the a is inside the parentheses and so the exponent of 3 outside the parentheses also applies to the a as well as to the b3.
If they are you subtract the exponent in the denominator from the exponent in the numerator. Thus x3 x -1 x4. A n a a.
Dividing fractions with exponents. There is a focus on the reasoning behind the exponent rules as part of this practice so students will be better able to apply these rules with negative exponents. Power Rule Powers to Powers.