K where a b a. Find one factor by making use of the Remainder Theorem Divide the polynomial by the factor we found thus giving us a simpler polynomial to work with Find one factor of the simpler polynomial and divide once again Continue until we get to a trinomial which we can usually factor easily.

Factoring Polynomials Using The Gcf
Px x 5x 2x 5 The roots for this polynomial are x 5 -2 and -5.
Finding factors of polynomials. Find the all of the factors of d. Learn how to find all the zeros of a polynomial given one rational zero. Zeroes of polynomials when represented in the form of another linear polynomial are known as factors of polynomials.
Using the Factor Theorem in Finding the Factors of Polynomials With Examples Factor Theorem Proof. This online calculator writes a polynomial as a product of linear factors. Find one factor that.
Further factoring furnishes fitting fanswerser answers. Our other factor is x 2 7x 10. The Degree of a Polynomial with one variable is.
For polynomials in one variable finding the factors is equivalent to finding the roots. If x c is a factor of P x then the remainder R obtained by dividing f x by x r will be 0. The following methods are used.
All you want to provide is the given inputs in the below box tap on the calculate button to get the final result along with a detailed solution. Rearrange the expression so its in the form of ax3bx2cxd. If one root is 5 that means x 5 is a factor.
The largest exponent of that variable. A common method of factoring numbers is to completely factor the number into positive prime factors. We explain Linear Factors of Polynomials with video tutorials and quizzes using our Many WaysTM approach from multiple teachers.
If the equation is a trinomial it has three terms you can use the FOIL method for. Lets say youre working with the equation. Able to display the work process and the detailed step by step explanation.
For example 2 3 5 and 7 are all examples of prime numbers. The first step in solving a polynomial is to find its degree. Order of Operations Factors Primes Fractions Long Arithmetic Decimals Exponents Radicals Ratios Proportions Percent Modulo Mean Median Mode Scientific Notation Arithmetics Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Pi Product Notation Induction.
For example the greatest common factor of 3x2 6xy 12xy2 is 3x. The calculator will try to factor any polynomial binomial trinomial quadratic etc with steps shown. After factorisation of a given polynomial if we divide the polynomial with any of its factors the remainder will be zero.
This lesson explains how knowing the linear factors of a polynomials allows us to determine their zeros. Divide both sides by x. To find the factors of a polynomial identify the greatest common factor of all terms and reference common variables as well.
You have multiple factoring options to choose from when solving polynomial equations. Factoring Using the Free Term 1. Factoring monomials common factor factoring quadratics grouping and regrouping square of sumdifference cube of sumdifference difference of squares sumdifference of cubes the rational zeros theorem.
A prime number is a number whose only positive factors are 1 and itself. Examples of numbers that arent prime are 4 6 and 12 to pick a few. We can use synthetic division to find the rest.
Factorizing a Polynomial by Applying the Factor. The multiple factor is also a factor of the polynomials derivative with respect to any of the variables if several. X 3 - 4x 2.
The calculator accepts both univariate and multivariate polynomials. Polynomial Factoring Calculator shows all steps supports polynomials with both single and multiple variables show help. For a polynomial no matter how many terms it has always check for a greatest common factor GCF first.
When we know the degree we can also give the polynomial a name. The constant d is going to be the number that doesnt have any variables such. A polynomial is an expression of the form axn bxn-1.
X 2x 5 That means our full polynomial is. Also in this process we factor the polynomial by finding its greatest common factor. Factoring Over Complex Numbers Factoring Over Complex Numbers is a free online tool that solves factoring polynomials over complex numbers just like that.
If two or more factors of a polynomial are identical then the polynomial is a multiple of the square of this factor. Is a root of a polynomial if and only if is a factor of. A polynomial of degree has at most roots and so at most factors.
You also learned the formula for finding the area of any regular polygon if you know the length of one side and the apothem. Find the area by computing the half of the product of perimeter and apothem.

How To Find The Area Of Irregular Polygons Video Lesson Transcript Study Com
220 cm 2.
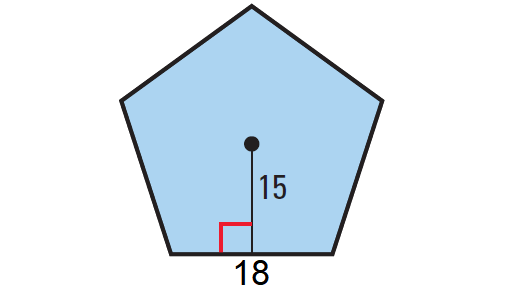
Finding the area of a regular polygon. As shown below this means that we must find the perimeter distance all the way around the hexagon and the measure of the apothem using right triangles and trigonometry. Area of Regular Polygon. A regular polygon is equilateral it has equal sides and equiangular it has equal angles.
An apothem is also used sometimes to find the area of a regular polygon. ½ x 44 x 10 cm 2. Area of a regular polygon The number of square units it takes to completely fill a regular polygon.
Know the correct formula. The area of any regular polygon is equal to half of the product of the perimeter and the apothem. The first two problem explains how to calculate.
A n s a 2 A n s a 2 where n n is the number of sides s s is the length of one side and a a is the apothem. All vertices of a regular polygon lie on a common circle the circumscribed circle ie they are concyclic points. I thought it could be the order of operations or how the user input was being handled but they seem ok.
So the expected result is supposed to be 7369017017488385 but I get 7269017017488385. Finding the area of regular polygon when the SIDE and APOTHEM are known. Use this calculator to calculate properties of a regular polygon.
One of these smaller triangles covers 110 of the pentagons area. Regular polygons may be either convex or starIn the limit a sequence of regular polygons with an increasing number of sides approximates a circle if the perimeter or area is fixed or a regular apeirogon effectively a straight line. Multiply to find the area of the pentagon.
To find the total area multiply the area of the smaller triangle by 10. Now click the button Solve to get the regular polygon area Step 3. The area of any.
This geometry video tutorial explains how to calculate the area of a regular polygon using a simple formula. Area of a regular polygon Calculating the area of a regular polygon can be as simple as finding the area of a regular triangle. Apothem is a segment that joins the polygons center to the midpoint of any side and it is perpendicular to that side.
Number of sides n n3456. Area of regular polygon where p is the perimeter and a is the apothem. Polygons can be regular or irregular.
To find the area of a regular hexagon or any regular polygon we use the formula that says Area one-half the product of the apothem and perimeter. N5 S 3 Step 2. Calculating the Area 1.
To find the area of a regular polygon you use an apothem a segment that joins the polygons center to the midpoint of any side and that is perpendicular to that side segment HM in the following figure is an apothem. The procedure to use the area of regular polygon calculator is as follows. Area of a Hexagon.
Find the area of a regular polygon with perimeter of 44 cm and apothem length of 10 cm. Area of Regular Polygons using Apothem The printable worksheets for grade 7 and grade 8 provide ample practice in finding the area of a regular polygon using the given apothem. Enter the number of sides and side length in the input field Example.
In Euclidean geometry a regular polygon is a polygon that is equiangular all angles are equal in measure and equilateral all sides have the same length. Four different ways to calculate the area are given with a formula for each. In our example the area of the whole pentagon 84 x 10 84 square units.
Regular polygons have equal side lengths and equal measure of angles. Here is the formula Im using to find the area of a regular polygon given 1 side here is the expected output that i am supposed to get. The perimeter is the combined length of the outline of any two-dimensional figure.
Interior angles of polygons To find the sum of interior angles in a. Enter any 1 variable plus the number of sides or the polygon name. As we know Area A ½ x p x a here p 44 cm and a 10 cm.
If the angles are all equal and all the sides are equal length it is a regular polygon. The apothem of a regular polygon is the shortest distance from the center point to one of the. How to use the formula to find the area of any regular polygon.
Try this Drag the orange dots on each vertex to resize the polygon. There are three methods of calculating the area of a regular polygon. A area P perimeter π pi 31415926535898 square root Calculator Use Polygon Calculator.
Finally the area of the regular polygon will be displayed. Area Calculates the area perimeter angle and number of diagonal lines of a regular polygon given the side.
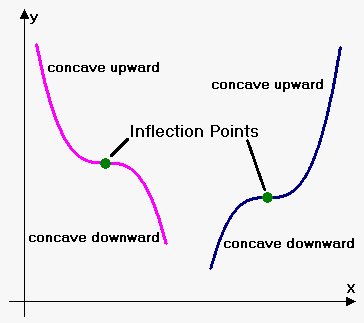
Inflection points are points where the function changes concavity ie. The calculator will find the intervals of concavity and inflection points of the given function.
Inflection Points On Emathhelp
In view of the above theorem there is a point of inflection whenever the second derivative changes sign.

Finding concavity and inflection points. MATH 124 Fall 2011 42 Inflection Points Concavity and Inflection Points A point at which the graph of a function f changes concavity is called an inflection point of f. First the second derivative is f x 12 x 24. That is where it changes from concave up to concave down or from concave down to concave up just like in the pictures below.
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. If p is an inflection point of f then either f 00 p 0 or f 00 is undefined at p. 54 Concavity and inflection points.
We know that the sign of the derivative tells us whether a function is increasing or decreasing. By using this website you agree to our Cookie Policy. Concavity and Second Deriv.
Also explain it geometrically. Find the inflection points and intervals of concavity up and down of f x 2 x 3 12 x 2 4 x 27. Free functions inflection points calculator - find functions inflection points step-by-step This website uses cookies to ensure you get the best experience.
Steps 2 and 3 give you what you could call. E3x is e 3 x and e 3x is e 3 x. Example 1 For the graph of f x given below indicate the approximate locations of all.
Then test all intervals around these values in the second derivative of the function. In determining intervals where a function is concave upward or concave downward you first find domain values where f x 0 or f x does not exist. In general you can skip parentheses but be very careful.
You da real mvps. F x 6 x 6 x 0 x 0 and consequently the original function has an inflection point in x 0. Determine whether the second derivative is undefined for any x- values.
1 per month helps. They can be found by considering where the second derivative changes signs. Thanks to all of you who support me on Patreon.
Definition of Point of Inflection A point P on the graph of y f x is a point of inflection if f is continuous at P and the concavity of the graph changes at P. HW 53 Concavity Points of Inflection Name_____ ID. Set the second derivative equal to zero and solve.
For example when f x 0 f x is increasing. How to Locate Intervals of Concavity and Inflection Points Find the second derivative of f. This calculus video tutorial shows you how to find the intervals where the function is increasing and decreasing the critical points or critical numbers re.
Concavity of a Function. Thus solving 12 x 24 0 there is just the one inflection point 2. If a function changes from concave upward to concave downward or vice versa around a point it is called a point of inflection of the function.
The graph of a curve is said to be concave up over an interval in which the second derivative is positive. The process to find the inflection points the same as finding the maximums and minimums is an algorithmic and very mechanical process. The sign of the second derivative f x tells us whether f is increasing or decreasing.
Find points of inflection of functions given algebraically. The concavity of a curve can be determined by the second derivative. Also be careful when you write fractions.
If youre seeing this message it means were having trouble loading external resources on our website. 1x2 ln x is 1 x 2 ln x and 1 x2 ln x is 1 x 2 ln x. Plot these numbers on a number line and.
We have seen that if f is zero and increasing at a point then there is a local minimum at the point and if f is zero and decreasing at a point then there is a local maximum at the point. In general you can skip the multiplication sign so 5 x is equivalent to 5 x. B Find the concavity point of inflection of fue-unn Where n658.
From being concave up to being concave down or vice versa. To find the point from which we are going to derive the derivative function and equal it to zero. In similar to critical points in the first derivative inflection points will occur when the second derivative is either zero or undefined.
1 Date_____ Period____ p j2k0_1M6y PKTutPat qSyoafktbwwamrzeQ BLwLCOe l cAVlVls yriqgChgtxsE rqefsDeJrLvceGdl-1-For each problem find the x-coordinates of all points of inflection and find the open intervals where the function is concave up and concave down. To find a point of inflection you need to work out where the function changes concavity.
T w Now make an educated guess for the limit. And in fact when x gets to 1 the functions value actually is 6.
Functions Limits Of Functions From Tables And Graphs Youtube
Intuitively we know what a limit is.
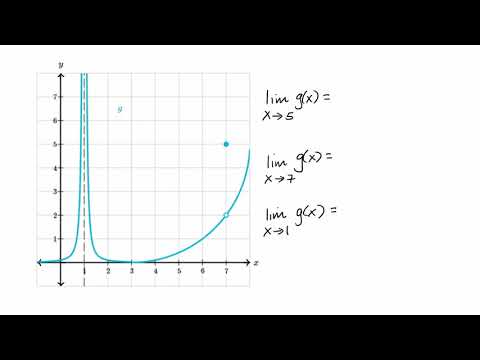
Finding a limit graphically. Youll learn about the derivatives and youll know that its impossible to have two values. Limx c fx This is called the right handed limit. Find a limit using a graph.
Displaystyle lim_ x to 2 dfrac x-2 x2-4 x2lim. Hide Plot. Subtracting the numerators gives youwhich then simplifies to Use the rules for fractions to simplify further.
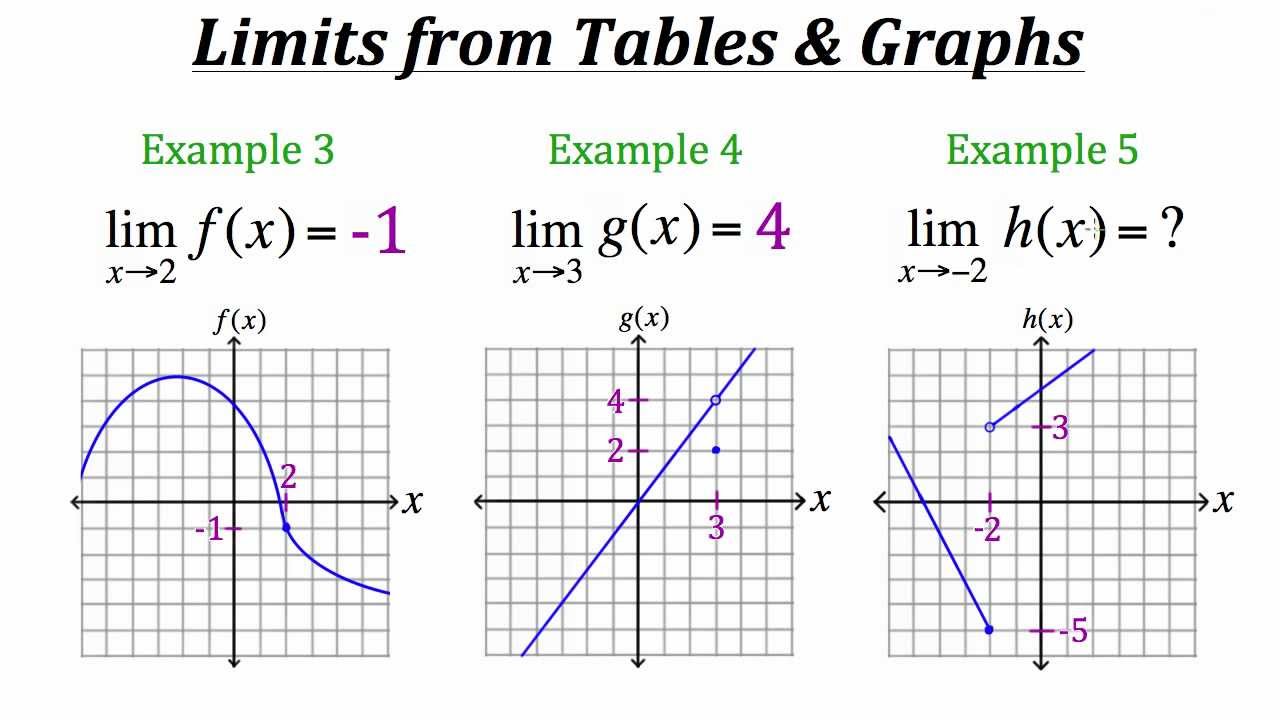
X 19 199 1999 2 𝑥 t 𝑥2 v. If we are interested in what is happening to the function fx as x gets close to some value c from the left we write. This calculus video tutorial explains how to evaluate limits from a graph.
Lim x 2 x 2 x 2 4. X 21 201 2001 2 𝑥 t 𝑥2 v. For example follow the steps to find the limit.
BEEBETTER at wwwtutorbeetv Limits Evaluating Functions Graphically I Worksheet 2 Evaluating Limits Graphically I Use the graph below to evaluate the following limits. You can see that as the x -value gets closer and closer to 1 the value of the function f x approaches 6. It explains how to evaluate one sided limits as well as how to evaluate the funct.
Free limit calculator - solve limits step-by-step. Find the LCD of the fractions on the top. Match expressions for limits at infinity with graphical behavior.
Examine the graph to determine whether a right-hand limit exists. If we are interested in what is happening to the function fx as x gets close to some value c from the right we write. And if the left limit and the right limit is different there will be two slopes which are not possible.
Examine the graph to determine whether a left-hand limit exists. Distribute the numerators on the top. Limit start subscript x to 2 end subscript start fraction x minus 2 divided by x squared minus 4 end fraction.
1 per month helps. Youll have to find the slope of the tangent line at the certain point of x. This website uses cookies to ensure you get the best experience.
At the open circle the coordinate displays as 2 undefined. Limxc-f x L to denote the limit of f x as x approaches c from the left is L limxcf x L to denote the limit of f x as x approaches c from the right is L limxcf x L to denote the limit of f x as x approaches c is L. Find a limit using a table.
10 Examples of finding limits graphically review. Finding the limit of a function graphically. Get access to all the courses and over 150 HD videos with your subscription.
02439 02494 02499 025. Finding Limits Graphically DRAFT. Limx c fx.
02564 02506 02501 025. Use a table of values to estimate the limit numerically. Find the limit as x approaches 1 Finding Limits Graphically DRAFT.
11th - 12th grade. You da real mvps. If youre seeing this message it means were having trouble loading external resources on our website.
Spring 2016 Calculus I Section 12 part 1. By using this website you agree to our Cookie Policy. Finding Limits Graphically limxc-fx L to denote the limit of fx as x approaches c from the left is L limxcfx L to denote the limit of fx as x approaches c from the right is L limxcfx L to denote the limit of fx as x approaches c is L.
We cannot define limit as two values. A car can go only so fast and no faster. Thanks to all of you who support me on Patreon.
Add or subtract the numerators and then cancel terms. 9 Examples of finding limits graphically one and two sided limits. 3 Examples of finding limits going to infinity graphically.
In the preceding figure. 11th - 12th grade. Monthly Half-Yearly and Yearly Plans Available.
If the two one-sided limits exist and are equal then there is a two-sided limitwhat we normally call a limit If there is a point at x a then f a is the.